Profinite Groups
Introduction
Profinite groups are Hausdorff compact and totally disconnected topological groups.
They are determined by their finite images under continuous homomorphisms: a profinite group is the inverse limit of its finite images.
For an abstract (infinite) group $G$, the normal subgroups of finite index give rise to a topology on $G$. The completion of $G$ with respect to this topology is a profinite group, the profinite completion of $G$.
Profinite groups appear naturally as the Galois groups of infinite Galois field extensions.
The first comprehensive account on profinite groups was given in
- J.-P. Serre, Cohomologie Galoisienne, Lecture Notes in Mathematics 5, Springer, Berlin 1964.
Modern accounts on the subject are
-
John S. Wilson, Profinite Groups, London Mathematical Society Monographs 19, Oxford University Press, New York 1998.
-
Luis Ribes and Pavel Zalesskii, Profinite Groups, 2nd ed., Ergebnisse der Mathematik und ihrer Grenzgebiete 40, Springer, Berlin 2010.
Inverse Limits (aka Projective Limits)
Basic Concepts
Definition. A set $I = (I, \leq)$ is a directed poset if $\leq$ is a partial order on $I$ (that is a reflexive, transitive and antisymmetric binary relation) and if $\leq$ is directed: for each $i, j \in I$ there is a $k \in I$ with $i, j, \leq k$.
Examples.  .
$(\mathbb{N}, \leq)$.
The subgroup lattice of a finite group $G$ with respect to $\subseteq$.
.
$(\mathbb{N}, \leq)$.
The subgroup lattice of a finite group $G$ with respect to $\subseteq$.
Note. Any poset $(I, \leq)$ (directed or not) is a category, with objects $I$ and morphisms $i \to j$ if $i \leq j$. An inverse system over a directed poset $I$ in a category $C$ is a contravariant functor $F \colon I \to C$.
Definition. An inverse system of topological spaces over a
directed poset $I$ is a collection $\{X_i: i \in I\}$ of topological
spaces with continuous maps $\phi_{ij} \colon X_i \to X_j$, for $i
\geq j$ (!), such that $\phi_{ii} = \mathtt{id}_{X_i}$ and the diagram
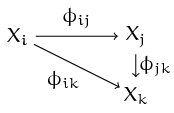 commutes for all $i \geq j \geq k$.
commutes for all $i \geq j \geq k$.
Examples. The constant inverse system on $I$ has $X_i = X$ and $\phi_{ij} = \mathtt{id}_X$ for all $i,j \in I$.
An example of an inverse system of finite groups is given by $I = \mathbb{N}$, $p$ prime, $G_i = \mathbb{Z}/p^i \mathbb{Z}$ and $\phi_{ij} \colon n + p^i \mathbb{Z} \mapsto n + p^j \mathbb{Z}$. This is an inverse system of finite groups.
Definition. Suppose $Y$ is a topological space with continuous
maps $\psi_i \colon Y \to X_i$, $i \in I$. The maps $\psi_i$ are
called compatible if the diagram 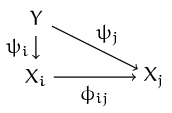 commutes, for all $i, j
\in I$.
commutes, for all $i, j
\in I$.
Note. In general, such an object $Y$ with compatible maps $\psi_i$ in a categroy $C$ is called a cone to the functor $F \colon I \to C$. An inverse limit is a universal cone.
Definition. A topological space $X$ with compatible maps $\phi_i
\colon X \to X_i$ is an inverse limit of the inverse system
$\{X_i\}$ if it satisfies the following universal property: for
all spaces $Y$ with compatible maps $\psi_i \colon Y \to X_i$, there
is a unique continuous map $\psi \colon Y \to X$ such that the diagram
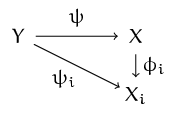 commutes, for all $i \in I$.
commutes, for all $i \in I$.
Notation. $X = \mathop{\varprojlim}\limits_{i \in I} X_i = \varprojlim X_i$. The maps $\phi_i \colon X \to X_i$ are called projections.
Inverse Limits Exist and are Unique
Proposition. Let $(X_i, \phi_{ij}, I)$ be an inverse system.
(a) If $(X, \phi_i)$ and $(Y, \psi_i)$ are both inverse limits of
$\{X_i\}$ then there exists a unique homeomorphism $\psi \colon Y
\to X$ such that the diagram  commutes, for all $i \in I$.
commutes, for all $i \in I$.
(b) The set $X = \{(x_i) \in \prod X_i : x_i^{\phi_{ij}} = x_j\}$ with $\phi_j \colon X \to X_j$, $(x_i) \mapsto x_j$ is an inverse limit of $\{X_i\}$. (Here $\prod X_i$ is equipped with the product topology, and $X$ with the subspace topology.)
Proof. (a) By the definition of an inverse limit, there exist continuous maps $\phi \colon X \to Y$ and $\psi \colon Y \to X$ such that the diagram
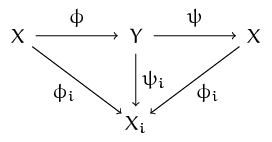 commutes, for all $i \in I$. Clearly, the diagram
commutes, for all $i \in I$. Clearly, the diagram 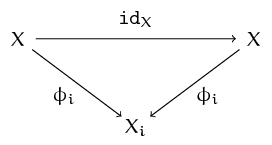 commutes.
But as the map $X \to X$ is unique, it follows that
$\phi \psi = \mathtt{id}_X$.
Similarly, $\psi \phi = \mathtt{id}_X$. Hence $\phi$ and $\psi$ are continuous
inverses of each other.
commutes.
But as the map $X \to X$ is unique, it follows that
$\phi \psi = \mathtt{id}_X$.
Similarly, $\psi \phi = \mathtt{id}_X$. Hence $\phi$ and $\psi$ are continuous
inverses of each other.
(b) It is easy to check that
- the $\phi_i$ are continuous,
- the $\phi_i$ are compatible (by construction),
- $X$ is universal: if $(Y, \psi_i)$ is a compatible cone, then $\psi \colon Y \to X$ defined by $\psi(y) = (\psi_i(y))$ is continous, and unique as any map $\psi’ \colon Y \to X$ with $\psi’ \phi_i = \psi_i$, for all $i \in I$, clearly satisfies $\psi’(y)_i = \psi_i(y) = \psi(y)_i$.